Résultats de thermodynamique
Un calcul simple donne l'énergie "Electronic Energy" Eel (qui contient en fait aussi la répulsion nucléaire (VN/N)). Un calcul de hessien permet d'obtenir les élements permettant de calculer des corrections conduisant à l'enthalpie et à l'enthalpie libre; à une température T (en K). Les couleurs employées ci-dessous pour les variables doivent vous guider dans l'extrait montré en bas. On obtient cet extrait en téléchargeant l'output, ou avec le bouton Thermo (il arrive qu'il "bug").
Corrections
A partir de l'énergie "Electronic Energy" Eel.
La correction pour obtenir l'énergie interne à 0 K (U0) est simplement l'ajout de l'énergie de point zéro (Zero Point Energy) : U0=Eel+ZPE.
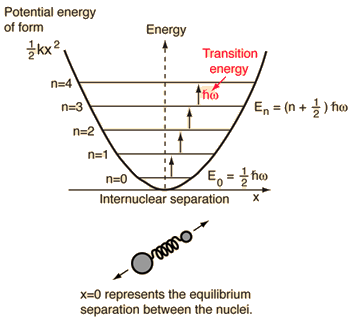
- ZPE est la somme des contributions des vibrations à 0 K (obtenue dans l'approximation harmonique ( ∑i 1/2 ℏωi)).
La correction pour obtenir l'énergie interne à 298.15 K (U298), est (hélas) notée E, presque comme l'énergie interne Eel. On a U298=Eel+E
- La correction E contient, en plus de ZPE, d'autres corrections thermiques électronique (0), de translation (3/2 x kBT), rotation (3/2 x kBT), et vibration (gaz parfait).
La correction pour obtenir l'enthalpie à 298 K (H298) est notée H. On l'applique simplement sur l'énergie électronique : H298=Eel+H.
- Cette correction diffère de la précédente par l'ajout de RT: On a la relation H298=U298+PV, ce qui pour n molécules revient à H298= U298+nRT (approximation du gaz parfait). A la température de 298.15 K et ramené à une mole, on a nRT=kBT=2.479 kJ/mol. Cette valeur ne dépend que de T, et à température constante ... est une constante.
La correction pour obtenir l'enthalpie libre à 298 K (G298) est notée G. On l'applique simplement sur l'énergie électronique :G298=Eel+G.
- Elle contient en particulier le terme entropique à 298.15 K: G298=H298-TS
S est l'entropie (donnée par GAMESS en J et non kJ comme les autres valeurs).